Inside the matrix: A look into the math behind AI

Introduction

Matrices are omnipresent in math and computer science, both theoretical and applied. They are often used as data structures, such as in graph theory. They are a computational workhorse in many AI fields, such as deep learning, computer vision and natural language processing. Why is that? Why would a rectangular array of numbers, with famously unintuitive multiplication rules, be so prevalent in AI?

AI methods (with emphasis on machine learning) are all about processing multi-dimensional data. A lot of that processing is done in a linear way - input data points are multiplied by scalars and added together to create output data. While that sounds limiting, a lot can be achieved with just that, for example:

• Linear layers in neural networks (excluding possibly non-linear activations)
• Principal component analysis
• Word embeddings
• Image processing

This particular kind of processing data has a name in mathematics - linear map, which is a concept from linear algebra. I will formally define it later in this blog. For now it suffices to say that you can represent any linear map as a matrix, and matrix operations are intimately connected to operations on linear maps. This is the main reason why matrices are so ubiquitous in AI.

While you don't necessarily need to know linear algebra to do machine learning, it is very helpful to have a good intuition for the concepts. This blog is an attempt to demystify matrices and linear algebra surrounding them in a way that strikes a balance between mathematical rigor and intuitive understanding. Contrary to most introductory material on the subject, we won't restrict ourselves to the usual Rn spaces, but I'll still give examples in R2 and R3 for clarity. If you don't know what R², R³ and Rⁿ are, don't worry - we'll get to that.

I will start with formally defining what a matrix is. We will gradually build up to understanding matrix multiplication, and by the end of the article we will have covered all the necessary concepts.

Definition of a matrix

A matrix is a rectangular array of numbers. The numbers are called elements of the matrix. The horizontal lines of elements are called rows, the vertical lines are called columns.

There are many operations we can perform on matrices, but for the purpose of this article we only need to know three:

• Addition: Element-wise addition, only matrices of the same dimensions can be added
• Scalar multiplication: Multiplying each element by a scalar
• Matrix multiplication: Multiplying two matrices, resulting in a matrix with dimensions equal to the number of rows in the second matrix and number of columns in the first matrix

The first two operations are pretty straightforward, but matrix multiplication is a bit more complex. There are several algorithms to do it, all resulting in the same end product.

One of the most common algorithms is this: For element in j-th row and k-th column of the resulting matrix, take the element-wise product of j-th row of the first matrix and k-th column of the second matrix, and sum all the elements of the resulting vector.

Why is matrix multiplication not simply element-wise (which actually exists and is called Hadamard product)? What is the intuition behind it? To answer that, we need to understand several concepts from linear algebra.

What is a vector?

A vector has many definitions. Perhaps the most well known is the one from physics: an arrow in space with a direction and a magnitude, usually represented as coordinates in a space.

If you are a programmer, you might know it as an array-like data structure, that is an ordered collection of elements. Both of these definitions are most likely known to you if you are working with AI systems, in which vectors often play a crucial role, e.g. as features in a dataset or as low-dimensional representations of high-dimensional data (embeddings).

What interests us here is the mathematical definition: A vector is an element of a vector space. What is a vector space then?

To avoid spelling the whole mathematical definition here, it suffices to say that a vector space is a set of elements with following properties:

• It is possible to add any two elements and the result is also in the set.
• It is possible to multiply any element by a scalar (a real number) and the result is also in the set.
• There exists an element called zero vector, which is such that adding it to any element does not change the latter.

These two operations are connected by a distributive property, which states that scalar multiplication of a sum is the sum of scalar multiplications: a * (u + v) = a * u + a * v.

As you have probably noticed, this is analogous to the operations of addition and multiplication on real numbers. The important thing to note is that the vector space definition does not require the vector by vector multiplication to be defined. It is defined for some vector spaces, but we won't concern ourselves with it in this blog.

All of that is pretty abstract, so let's consider some examples. Possibly the most well known vector spaces are R² and R³, which are spaces of vectors with 2 and 3 coordinates respectively. The generalization of those is Rⁿ, which is a space of vectors with n coordinates. The elements (vectors) of those spaces have a geometric interpretation as arrows or points. Notice how this aligns with the interpretation of vectors as known from physics.

Linear combination of vectors, span and linear independence

We know that vectors can be added and multiplied by scalars. A linear combination of vectors is a sum of scalar multiples of those vectors. Consider these examples in R² and R³:

A span of a finite set of vectors is a set of all possible linear combinations of those vectors. Geometrically, a span of one vector in R² and R³ is a line through the origin (all scalar multiples of the vector), while a span of two vectors might be a plane through the origin (which is the whole space in case of R²).

Why might? Consider two vectors lying on the same line. No matter what scalar coefficients we take for the linear combination, the result will lie on the same line. Their individual spans are identical to the span of the set of those two vectors. We say that those two vectors are linearly dependent.

Let's consider a set of three vectors in R³. They can either all lie on the same line, all lie on the same plane, or they can be such that their span is the whole space. In the first two cases, the vectors are linearly dependent, in the last case they are linearly independent. Two vectors in R² spanning the whole space are also linearly independent.

Rigorously speaking, a set of vectors in vector space is linearly independent if no vector in the set can be written as a linear combination of the other vectors in the set (in other words, it does not lie in the span of the rest of the vectors). Intuitively, vectors are linearly independent if each one of them contributes a unique "direction" to the span.

Linearly independent vectors have a very important property: each vector in their span can be uniquely represented as a linear combination of those vectors.

Basis

Not all vector spaces can be spanned by a finite set of vectors. For example, the space of all polynomials (which with proper definition of addition and scalar multiplication is valid vector space) is infinite-dimensional, because no matter how many polynomials we have, we can always find a polynomial that has a higher degree than all of them.

Contrarily, if we can find a finite set of vectors that spans the whole space, we say that the vector space is finite-dimensional. Only these spaces are relevant for the purposes of this blog.

Every finite-dimensional vector space has a basis. A basis is a set of linearly independent vectors that span the whole space. In R², a basis can consist of two non-collinear vectors. In R³, a basis can consist of three vectors that do not lie on the same plane. Note that a basis is not necessarily unique - e.g. in Rⁿ, we can choose different vectors that will still span the same space and be linearly independent.

Notice how I stated that a basis in R² consists of two vectors, while in R³ it consists of three vectors. A set of three vectors in R² is guaranteed to be linearly dependent, so it cannot be a basis. On the other hand, one vector cannot span R². Likewise, we cannot find four linearly independent vectors in R³, but less than three vectors cannot span R³.

Skipping the proof, it is a true statement that every basis of a finite-dimensional vector space has the same number of vectors. This number is called the dimension of the vector space. By this, Rⁿ has a dimension of n, which plays nicely with our geometric interpretation of Rⁿ as n-dimensional space.

For Rⁿ, we define a standard basis as a set of n vectors, where each vector has exactly one non-zero coordinate, which is 1. For example, in R³, the standard basis is {(1, 0, 0), (0, 1, 0), (0, 0, 1)}.

Why do we care about a basis? Since a basis is a set of linearly independent vectors that span the whole space, any vector in that space can be uniquely represented as a linear combination of vectors from the basis. That means that for every finite-dimensional vector space, no matter how abstract or exotic, we can always represent any of its vectors as a list of numbers (coefficients of linear combination of chosen basis).

Linear maps

Now we are ready to define a linear map. A linear map (sometimes also called linear transformation), defined for vector spaces V and W, is a function that takes a vector from V as an input and returns a vector from W. It must satisfy two properties:

• Additivity: f(u + v) = f(u) + f(v)
• Homogeneity: f(a * u) = a * f(u)

These properties ensure that linear maps preserve the linear structure of vector spaces - parallel vectors remain parallel, and origin remains at the origin.

While it may seem that linear maps are a very restricted class of functions, they can be used to represent a wide variety of transformations. For example, a linear map in R² can be used to represent:

• Rotation
• Scaling
• Reflection
• Shearing
• Any combination of the above

One operation you cannot represent with a linear map is translation (moving every point by the same vector), since the origin must remain at the origin.

As mentioned in the introduction, they are also extremely prevalent in machine learning, e.g. in neural networks. While I am not going to prove this, the connections (weights) between linear layers are equivalent to linear maps from Rⁿ to R^m, where n is the dimension of the input and m is the dimension of the output. Since you can represent these connections as a matrix, it's a hint that matrices are intimately connected to linear maps. We'll come back to this later.

We can define a set of operations on linear maps (let T and S be linear maps, and c an arbitrary scalar):

• Addition: (T + S)(v) = T(v) + S(v)
• Scalar multiplication: (c * T)(v) = c * T(v)
• Composition: (T * S)(v) = T(S(v))

A very important property of linear maps is that a linear map is fully defined by its values on basis vectors, for a chosen basis of input space. Let's say we have a linear map T and a basis B = {b₁, b₂, ..., b_n} of input space V. For any v in V, we can write v as a linear combination of basis vectors: v = c₁ * b₁ + c₂ * b₂ + ... + c_n * b_n. Then T(v) = c₁ * T(b₁) + c₂ * T(b₂) + ... + c_n * T(b_n). This means that if we know what T does to each vector in the basis, we know what T does to any vector in the space.

Matrix as representation of linear map

We know that every linear map T: V -> W (where V has dimension n and W has dimension m) and for a chosen basis Bv = {v₁, v₂, ..., v_n} of V, T is fully defined by values of T(v₁), T(v₂), ..., T(v_n).

Let's take a closer look at one of those values, say T(v₁). We know that T(v₁) is a vector in W, so we can write it as a linear combination of a chosen basis of W: T(v₁) = d₁ * w₁ + d₂ * w₂ + ... + d_m * w_m. We can represent the coefficients of this linear combination as a list of numbers: [d₁, d₂, ..., d_m]. This list is uniquely determined by the linear map T and the chosen basis of V, and it is called the column vector representation of T(v₁).

We can do the same for T(v₂), T(v₃), and so on, up to T(v_n). In this way, we can associate with our linear map T a matrix A, where the j-th column is the column vector representation of T(v_j). This matrix A is called the matrix representation of the linear map T. That is, a matrix with m rows and n columns can be interpreted as a representation of a linear map from linear space of dimension n to linear space of dimension m. When representing a linear map with a matrix, choice of bases is important - different bases will yield different matrices. That is why when not clear from the context, we must specify the bases for both the input and output spaces.

It is important to note that such a matrix can be created for any linear map between finite-dimensional vector spaces - it is not limited to Rⁿ. The common misconception is that the columns or rows of such a matrix are vectors, but in general they are not - they are coefficients of linear combinations. It is a coincidence that in the case of T: Rⁿ -> R^m and if we choose the standard basis for R^m, the columns of the matrix representation are vectors in Rⁿ.

Matrix operations as operations on linear maps

If matrices represent linear maps, do the matrix operations represent operations on linear maps? It turns out that they do.

It is easy (albeit a bit tedious) to prove, that if A and B are matrices representing linear maps T and S, then:

• A + B represents the linear map T + S
• c * A represents the linear map c * T
• A * B represents the linear map T * S

Keep in mind that matrix multiplication is not commutative, i.e. A * B is not necessarily the same as B * A (even if both make sense dimension-wise).

• Matrix addition is only defined for matrices of the same dimensions, which is consistent with the fact that addition of linear maps is only defined for maps between the same spaces.
• Matrix multiplication by scalar is defined for any matrix, which is consistent with the fact that scalar multiplication of linear maps is defined for any linear map.
• Matrix multiplication is defined for any two matrices, provided that the number of columns in the first matrix is the same as the number of rows in the second matrix. This is consistent with the fact that composition of linear maps is only defined for maps where the output space of the first map is the same as the input space of the second map.

While adding and multiplying by scalar are pretty intuitive operations, matrix multiplication is not that obvious. It has actually been defined so that composition of linear maps is represented by multiplication of their matrices, which you are encouraged to verify.

Aside from linear map composition, matrix multiplication can be used to apply a linear map to a vector. Say we have a linear map T: V -> W represented by matrix A, and a vector v in V. First we need to represent v as a nx1 column matrix. We'll call it Mat(v). Then we can compute A * Mat(v), which will be a vector in W.

This type of matrix multiplication can be computed as follows, where a_j is the j-th column of A, while m_1j is the j-th element of Mat(v):

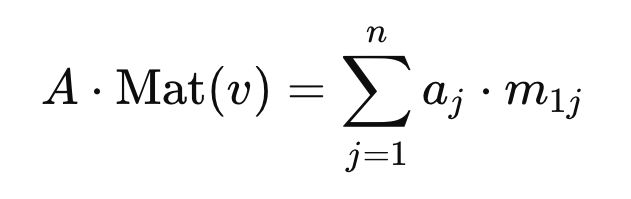
Applying T to v can be written as T(v) = c₁ * T(v₁) + c₂ * T(v₂) + ... + c_n * T(v_n).

Remembering that a column j of matrix A represents T(v_j), we can see that multiplying A by Mat(v) is indeed equivalent to applying T to v.

Conclusion

We have now covered all the necessary concepts from linear algebra to understand matrix multiplication. We have seen that matrices can be interpreted as representations of linear maps, and that matrix operations can be interpreted as operations on linear maps. We have also seen that matrix multiplication is not just an arbitrary operation, but rather a composition of linear maps. While this blog barely scratched the surface of math involved in creating AI systems, hopefully it gave you a good intuition on the subject of linear maps and matrices.

In conclusion, matrices are a fundamental tool in the AI toolkit, enabling efficient data manipulation and transformation. Whether you're building a simple linear regression model or a complex deep learning architecture, a solid grasp of matrix operations will empower you to create more effective and efficient AI solutions.